
Statistical Analysis Tools, Techniques and SPC Gage R&R (GR&R) and MSA (Measurement Systems Analysis) Minitab Error - * ERROR * Unbalanced Design - Unbalanced AnovaĭoE and ANOVA - 4 factor and 3 levels Taguchi design with 2 replicatesĪNOVA 3 level and 4 factors f and p values are not showing
MINITAB ANOVA SOFTWARE
Quality Assurance and Compliance Software Tools and Solutions Taguchi Design with ANOVA - 3 factors each with 3 levels The "trick" Minitab uses with blocks allows Minitab to recreate that different error structures because the math behind the analysis happens to work the same as with blocks.Ī screenshot of the partial datasheet that Minitab used in the example shows that the repeated measures were added in rows, not columns. Just as there is a difference in the error structure between the whole plot and the subplot, there is a difference in the error structure between subjects and within subjects. The analysis of a repeated measures design is similar to that of a split plot design. Unfortunately, the name repeated measures was given long ago and cannot be changed now. In the strict sense they are really replicates. At a minimum, these repeats include a time element of variation, and in a crossover design also include setup variation. Repeats in a repeated measures design are different than repeats in the normal sense. You are also correct that in normal designs, Minitab places replicates in additional rows and repeats in additional columns. Replicates see more chance for variation than repeats because replicates include setup variation and time variation which repeats do not see. In your first post, you have the correct sense of the difference between repeats and replicates under normal experiments. I think you are getting confused between the typical definition of repeats vs replicates, the repeats in repeated measures and the data entry structure used by Minitab to analyze repeated measures. Why do the degrees of freedom also increase that much for repeats? If the degrees of freedom also increase for repeats what’s the difference between repeats and replicates? The block doesn’t make that much of a change. Now I wonder that the degrees of freedom change the same way. I read in a book and on the side of minitab that for replicates you add new rows (so I assumed that you get more degrees of freedom) and for repeats you add new columns and write the results in the same rows (so I assumed that the degrees of freedom stay the same and only the total sum of squares (TSS), the sum of squares between groups (SSB) and the sum of squares within groups (SSW) change). Now I wonder that the degrees of freedom also increase that much if I have repeats. When you have replicates the degrees of freedom increase a lot because you made “truly separate” runs.
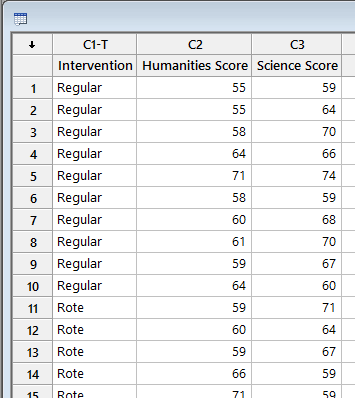
In this example the experimental block is called “dial”. So if I get it right the only difference between “repeats” and “replicates” for minitab is that you insert an experimental block. While trying to get the procedure right and running my own analysis I got two more questions. I didn't expect to get an answer that fast.


 0 kommentar(er)
0 kommentar(er)
